Ανατροπή κανόνων στην Ταινία του Μέμπιους
(Απόσπασμα Ομιλίας μου)
Και στο σημείο αυτό, αγαπητοί φίλοι, θα παρατηρήσω μιαν εξαίρεση σε όλους τούς κανόνες, που εφαρμόζονται στην Ταινία του Μέμπιους, την δισδιάστατη κατασκευή στον ευκλείδειο χώρο, το χώρο των τριών διαστάσεων, όπως τον γνωρίζουμε με τις αισθήσεις μας οι άνθρωποι. Κατ’ επέκταση, όπως παρατηρήσαμε και προηγουμένως στα παραδείγματα που συσχετίζουν την Ταινία του Μέμπιους με τη Φιάλη του Κλάιν, η ίδια εξαίρεση εφαρμόζεται και στη Φιάλη του Κλάιν.
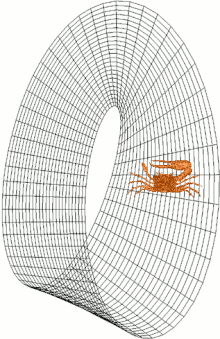
Πρώτα θα σας ξαναφέρω για λίγο στην αρχή της ομιλίας μου, όταν παρατηρήσαμε τη συμπεριφορά του κάβουρα που διατρέχει την Ταινία του Μέμπιους στις δυο διαστάσεις της. Θυμάστε ότι ο κάβουρας, που κινείται πάνω στην Ταινία, κάθε φορά που κάνει έναν πλήρη κύκλο αντιστρέφεται, δηλαδή η μεγάλη του δαγκάνα από αριστερά πάει δεξιά. Αποδείξαμε επίσης πώς και γιατί ο κάβουρας δεν έχει συναίσθηση και γνώση παρά μόνο των δύο διαστάσεων στο χώρο, των διαστάσεων της Ταινίας. Το ίδιο θα συνέβαινε, όπως είπαμε και αν είχαμε έναν άνθρωπο στην επιφάνεια της Ταινίας. Κανένας άνθρωπος παγιδευμένος στις δυο διαστάσεις της ταινίας δεν έχει συνείδηση του τρισδιάστατου χώρου μέσα στον οποίον βρίσκεται η ταινία. Ως εδώ καλά.
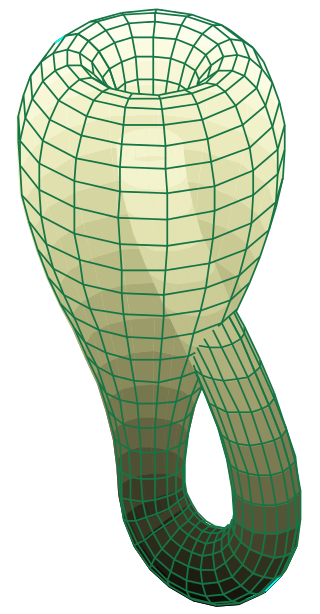
Με τον ίδιο τρόπο στη Φιάλη του Κλάιν αν ένας άνθρωπος διασχίσει την επιφάνειά της, ξέρουμε ότι μπορεί να φτάσει στο σημείο που ξεκίνησε αλλά θα είναι ανεστραμμένος στο χώρο του, με το κεφάλι κάτι και τα πόδια πάνω, αν είχε ξεκινήσει περπατώντας.
Κι ερχόμαστε τώρα στην εξαίρεση. Υπάρχει ένα είδος ανθρώπου σε μια συγκεκριμένη συνθήκη που θα αποδείξουμε τώρα ότι σε οποιοδήποτε σημείο της Ταινίας ή της Φιάλης και να βρίσκεται, έχει απόλυτη συνείδηση, γνώση, ενσυναίσθηση αλλά και διάφορα συναισθήματα ανεξάρτητα των δεδομένων συνθηκών αλλά και πολλές φορές δημιουργούμενα από αυτές.
Το είδος αυτό του ανθρώπου δεν ανήκει σε κάποια συγκεκριμένη φυλή, είναι πανανθρώπινο, ανήκει όμως σε συγκεκριμένο φύλο και ηλικία του ανθρώπου. Πρόκειται για τα Κορίτσια.
Τα κορίτσια η πόα της ουτοπίας, τα κορίτσια οι παραπλανημένες Πλειάδες, τα κορίτσια τ’ Αγγεία των Μυστηρίων, τα γεμάτα ως πάνω και τ’ απύθμενα, τα στυφά στο σκοτάδι και όμως θαύμα, τα γραμμένα στο φως και όμως μαυρίλα, τα στραμμένα επάνω τους όπως οι φάροι, τα ηλιοβόρα και τα σεληνοβάμονα.
Αυτά τα Κορίτσια, όπως ήδη θα διαπιστώσατε από τα λόγια του έγκριτου Νομπελίστα Οδυσσέα Ελύτη, δεν υπακούουν στους νόμους ούτε της Ευκλείδειας Γεωμετρίας ούτε της Τοπολογίας. Διαθέτουν δικούς τους χώρους και χρόνους. Χώρο πολυδιάστατο, αδύνατον ακόμα να ερευνηθεί και αποδειχθεί μαθηματικά από τους επιστήμονες. Και Χρόνο ιδιαίτερο, που τείνει να εξαλείψει την έννοια του χρόνου, όπως οι άνθρωποι τον γνωρίζουμε με τις αισθήσεις μας και από την κίνηση του ήλιου.
Όταν η Έρση και η Μυρτώ, για παράδειγμα, καταφέρνουν να ανθίσουν μέσα στην ουτοπία, πώς δε θα καταφέρουν να διασχίσουν την Ταινία του Μέμπιους ή τη Φιάλη του Κλάιν αναστρέφοντας τα αποδεδειγμένα δεδομένα τους;
Αν, επίσης, η Μαρίνα και η Ελένη αλλάζουν τις διαστάσεις του χώρου, ούσες γεμάτες ως πάνω και απύθμενες, έχουν φυσικά την ικανότητα να διασχίζουν τη Φιάλη του Κλάιν χωρίς να βρεθούν με το κεφάλι κάτω και τα πόδια πάνω.
Εφόσον η Ρωξάνη και η Φωτεινή είναι γραμμένες στο φως και όμως μαυρίλα, καταφέρνουν να γίνουν ηλιοβόρες και σεληνοβάμονες. Έχουν, δηλαδή, φτάσει σε κόσμους που η Φυσική μας δεν μπορεί να αγγίξει. Έχουν τη δύναμη και την ικανότητα εν ριπεί οφθαλμού να ακυρώσουν τους νόμους, τους οποίους εξετάζουμε και να αποτελέσουν την εξαίρεση στον κανόνα.
Το ίδιο συμβαίνει και με την Άννα, την Αλεξάνδρα και την Κύνθια, που, μέσα σε όλα τα άλλα χαρακτηριστικά τους, αν και στυφές στο σκοτάδι, είναι ένα θαύμα και σαν Αγγεία των Μυστηρίων έχουν την μαγική ικανότητα να μάς ακινητοποιούν.
Επίσης μια τρανταχτή απόδειξη της εξαίρεσης αυτού του Κόσμου στους κανόνες που μελετήσαμε, είναι η ενσυνείδηση. Ο Κόσμος των Κοριτσιών είναι ένας κόσμος μέσα στον οποίον αναπτύσσεται η συνείδηση του δεδομένου ατόμου και όλα τα συναισθήματα, από το πιο ευγενή έως τα πλέον ποταπά. Μέσα από αυτούς τους ανεπτυγμένους, πολύπλοκους, μυστικούς και ανεξερεύνητους ακόμα μηχανισμούς τα Κορίτσια γίνονται ενήλικες και εν δυνάμει Μητέρες.
Δεν θα σας κρατήσω για πολύ ακόμη. Θα μπορούσα να αναλύσω κάθε ιδιότητά τους αλλά σέβομαι το χρόνο σας. Σας αφήνω να ερευνήσετε μόνοι σας. Είναι φανερό ότι τα Κορίτσια έχουν άλλους νόμους στη Φύση.
Για τούτο και ξεπέρασαν τις Πλειάδες, όπως είδατε, γενόμενες παραπλανημένες Πλειάδες. Ούτε στους νόμους των Πλειάδων υπάκουσαν. Εξακολουθούν σε όλα τα μήκη και πλάτη τής γης, ανεξάρτητα από θρησκεία, οικογένεια, φυλή, πολιτική, οικονομία, από όλους τούς γήινους παράγοντες τέλος πάντων, να βρίσκονται σε ένα παράλληλο άγνωστο Σύμπαν, το Κορισύμπαν όπως το ονομάζω, ύστερα από εκτεταμένες έρευνες και παρατηρήσεις.
Από αυτό το Κορισύμπαν κάποια στιγμή θα βγουν – αν βγουν, γιατί ενδέχεται να παγιδευτούν δια βίου μέσα σ’ αυτόν τον Κόσμο – θα βγουν μόνον όταν γίνουν μητέρες. Τότε θα αναγκαστούν να σπάσουν έναν από τους βασικούς κανόνες του Κόσμου τους. Δεν θα είναι πλέον τα κορίτσια «στραμμένα επάνω τους όπως οι κάβοι» γιατί η προσοχή τους θα έχει στραφεί αλλού.
Σας ευχαριστώ για την παρουσία σας σήμερα εδώ.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Βοηθήματα που χρησιμοποιήθηκαν στη ομιλία:
ΠΟΙΗΣΗ
Οδυσσέας Ελύτης
Απόσπασμα από το Δοξαστικό στο «Άξιον Εστί», 1959
Τα κορίτσια η πόα της ουτοπίας
τα κορίτσια οι παραπλανημένες Πλειάδες
τα κορίτσια τ’ Αγγεία των Μυστηρίων
τα γεμάτα ως πάνω και τ’ απύθμενα
Τα στυφά στο σκοτάδι και όμως θαύμα
τα γραμμένα στο φως και όμως μαυρίλα
τα στραμμένα επάνω τους όπως οι φάροι
τα ηλιοβόρα και τα σεληνοβάμονα
Η Έρση, η Μυρτώ, η Μαρίνα
η Ελένη, η Ρωξάνη, η Φωτεινή
η Άννα, η Αλεξάνδρα, η Κύνθια
ΤΟΠΟΛΟΓΙΑ
Μία λωρίδα του Μέμπιους, ή Ταινία του Μέμπιους (διεθνώς: Möbius strip), είναι μια επιφάνεια με μόνο μία πλευρά (όταν εμφυτευθεί σε τρισδιάστατο ευκλείδειο χώρο) και μόνο ένα σύνορο. Η λωρίδα του Μέμπιους έχει την μαθηματική ιδιότητα να μην είναι προσανατολιζόμενη.
Στην τοπολογία, ένα κλάδο των μαθηματικών, η Φιάλη του Κλάιν ή το Μπουκάλι του Κλάιν, είναι ένα παράδειγμα μιας μη-προσανατολιζόμενης επιφάνειας. Είναι μια δισδιάστατη πολλαπλότητα πάνω στην οποία δεν μπορεί να οριστεί ένα σύστημα για τον προσδιορισμό ενός κάθετου διανύσματος. Με απλά λόγια, είναι μια μονόπλευρη επιφάνεια στην οποία, αν περπατήσει κανείς επάνω της, θα μπορούσε να φτάσει στο σημείο στο οποίο ξεκίνησε, αλλά ανάποδος, δηλαδή με το κεφάλι να είναι προς την κατεύθυνση την οποία ήταν τα πόδια του.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Το κείμενο έγραψε η Ανθή Ανδρεοπούλου, στο πλαίσιο του Συνεργείου Δημιουργικής Γραφής